Introduction to Diffusion

얼마 전 회사에서 Diffusion 리뷰 요청을 받고 Diffusion models의 원조격 논문인 Denoising Diffusion Probabilistic Models를 읽고 발표자료를 만들어 발표를 진행했다.
발표를 들어주신 분들께서는 아주 만족해 하셨지만 발표를 준비하는 과정은 꽤나 힘들었다. 아무래도 하나의 커다란 흐름의 시작이 됐던 논문인 만큼 내용도 매우 많고 수식이 범벅인데 증명도 잘 되어있지 않은 경우가 많아 한장한장 넘기기가 힘들었다. 하지만 읽으면서 너무 놀라운 아이디어들과 아름다운 수식의 연속에 놀라움을 금치 못했다. 잘 정리되어 있는 블로그나 유튜브 영상들이 많지만 나의 언어로 잘 정리해보았다. 개인적으로 초심자가 접근하기 쉽게 만들었다고 생각하고, 수식의 증명도 최대한 자세하게 작성했다.

개인적으로 논문을 너무 인상깊게 읽었고, 만든 슬라이드도 만족스러웠기 때문에 블로그 포스트로 저장해본다. (이미지로 업로드)

Introduction to Diffusion

Contents

Generative Models

GAN, VAE, Flow-based, Diffusion

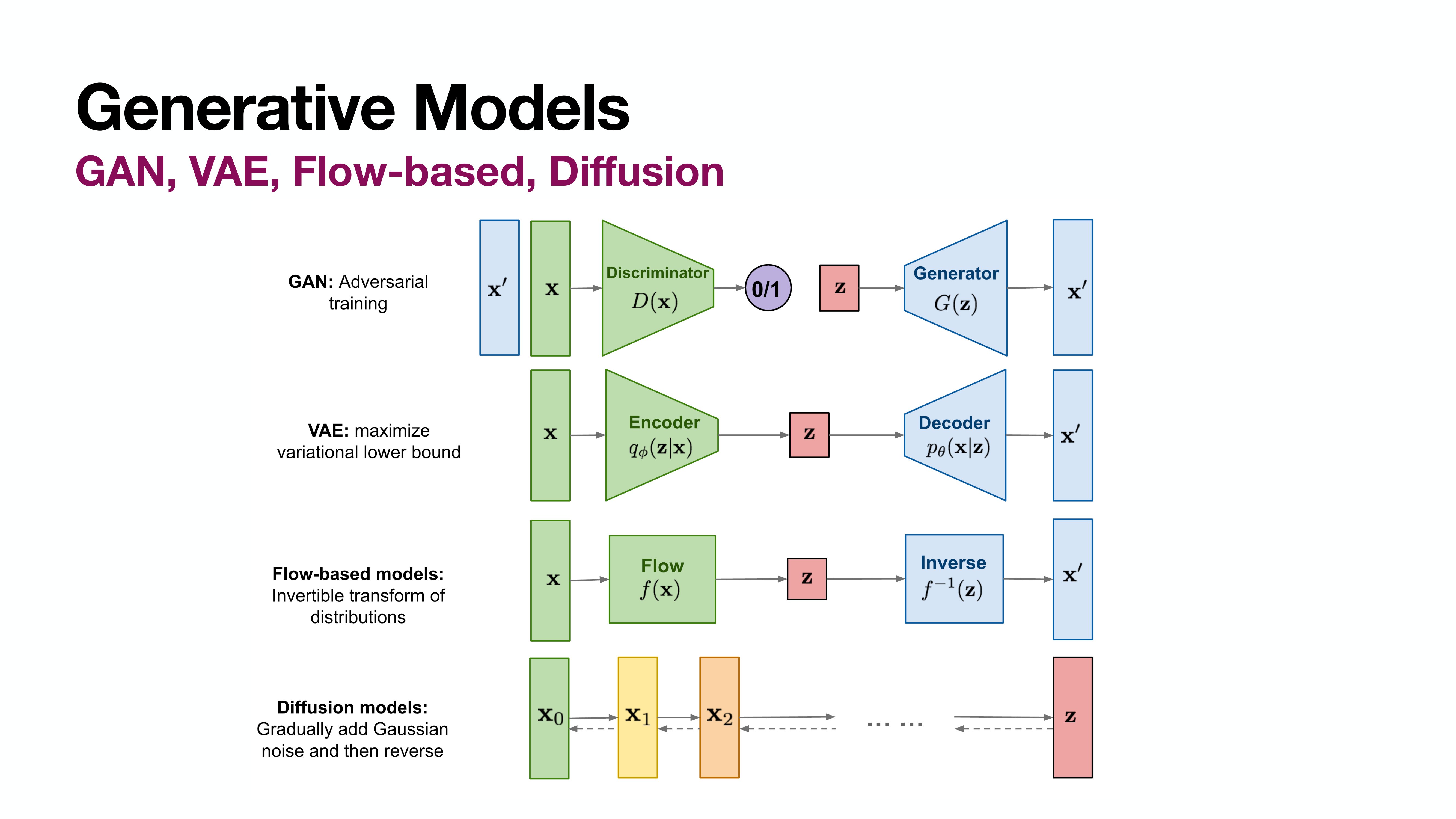
Diffusion이 메인 스트림으로 자리잡기 전에는 위쪽의 세가지 모델이 Generative model의 대표격이었다.

GAN은 Generator외에 Discriminator의 학습이 필요하다.
VAE는 Decoder외에 Encoder의 학습이 필요하다. 그리고 $\mathbf{z} \sim N(0, I)$를 보장하기 위한 장치들이 필요하다.
Flow-based model은 Encoder만 학습하여 이의 inverse를 Decoder로 활용하게 된다. 하지만 여전히 $\mathbf{z} \sim N(0, I)$를 보장하기 위한 장치들이 필요하다.

Diffusion은 오로지 Decoder만 학습한다. (Adeversarial loss를 활용하는 등 다양한 방법이 있긴 하겠다만.. 가장 단순한 방법만 보자면.) 그리고 Encoder의 학습이 없이도 $\mathbf{z} \sim N(0, I)$를 보장할 수 있다.

What is Diffusion?

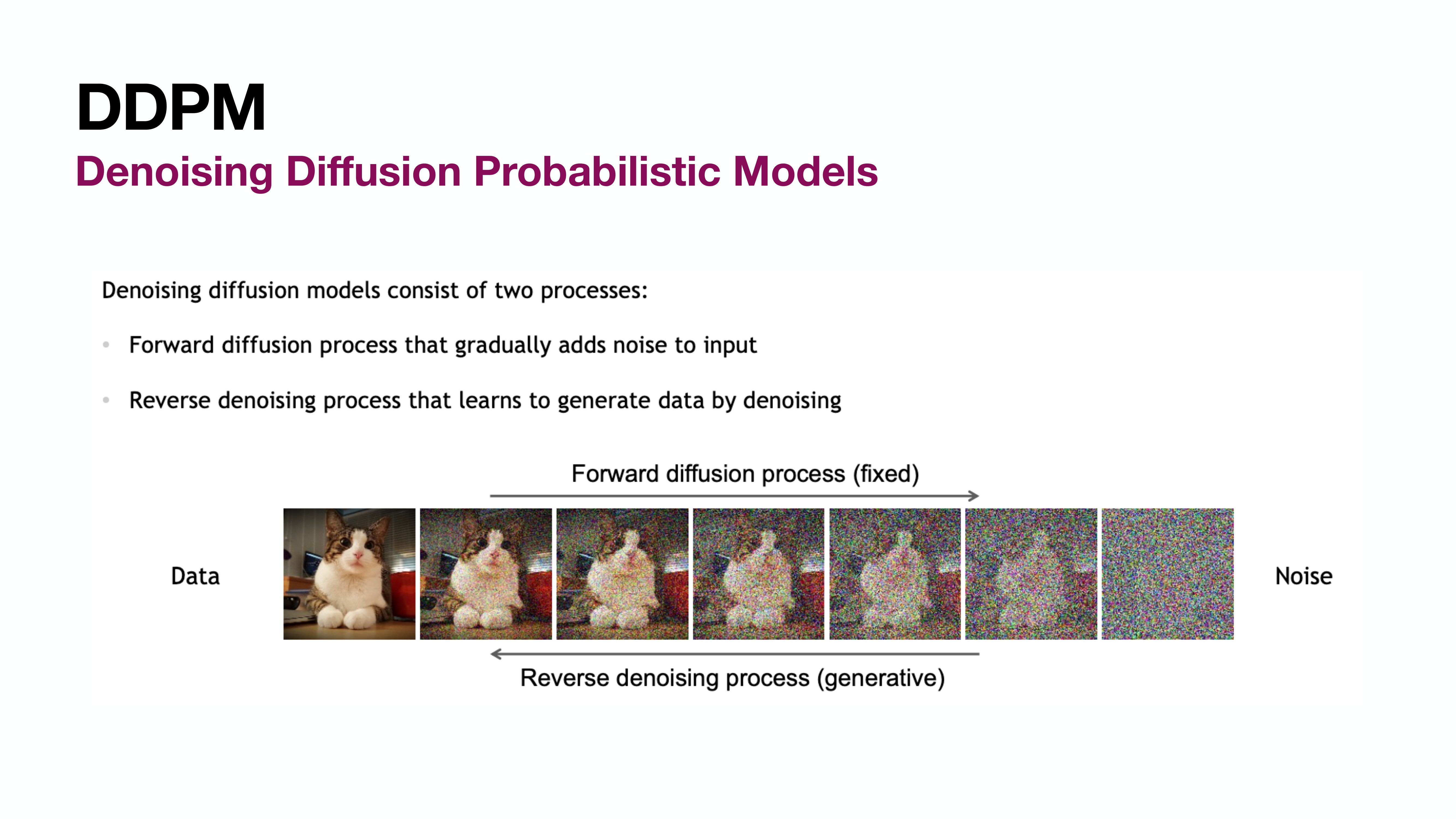
Denoising Diffusion Probabilistic Models (DDPM)

Forward Diffusion Process

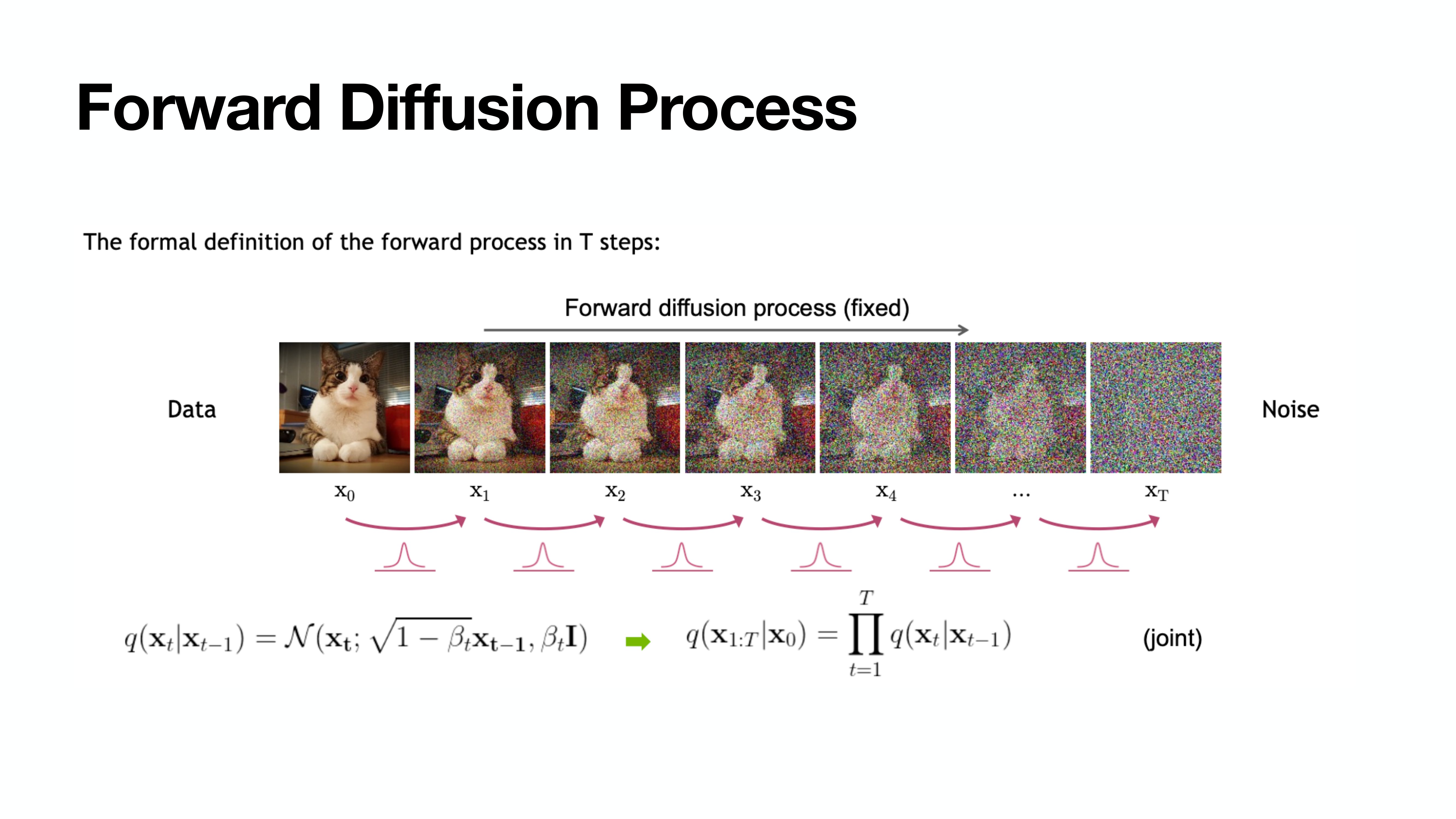
이때 $\beta$가 충분히 작다면 $q(\mathbf{x}_{t-1} \rvert \mathbf{x}_t)$도 Gaussian임이 알려져있다고 한다.
arXiv:1503.03585

$\beta$는 일종의 hyper parameter로, 필자는 튜토리얼에서 t가 커짐에 따라 1e-4부터 0.02까지 linear하게 증가하도록 설정했다. linear형태의 증가 뿐 아니라 sigmoid형태 등 다양하게 설정 가능하다.

Reverse Denoising Process

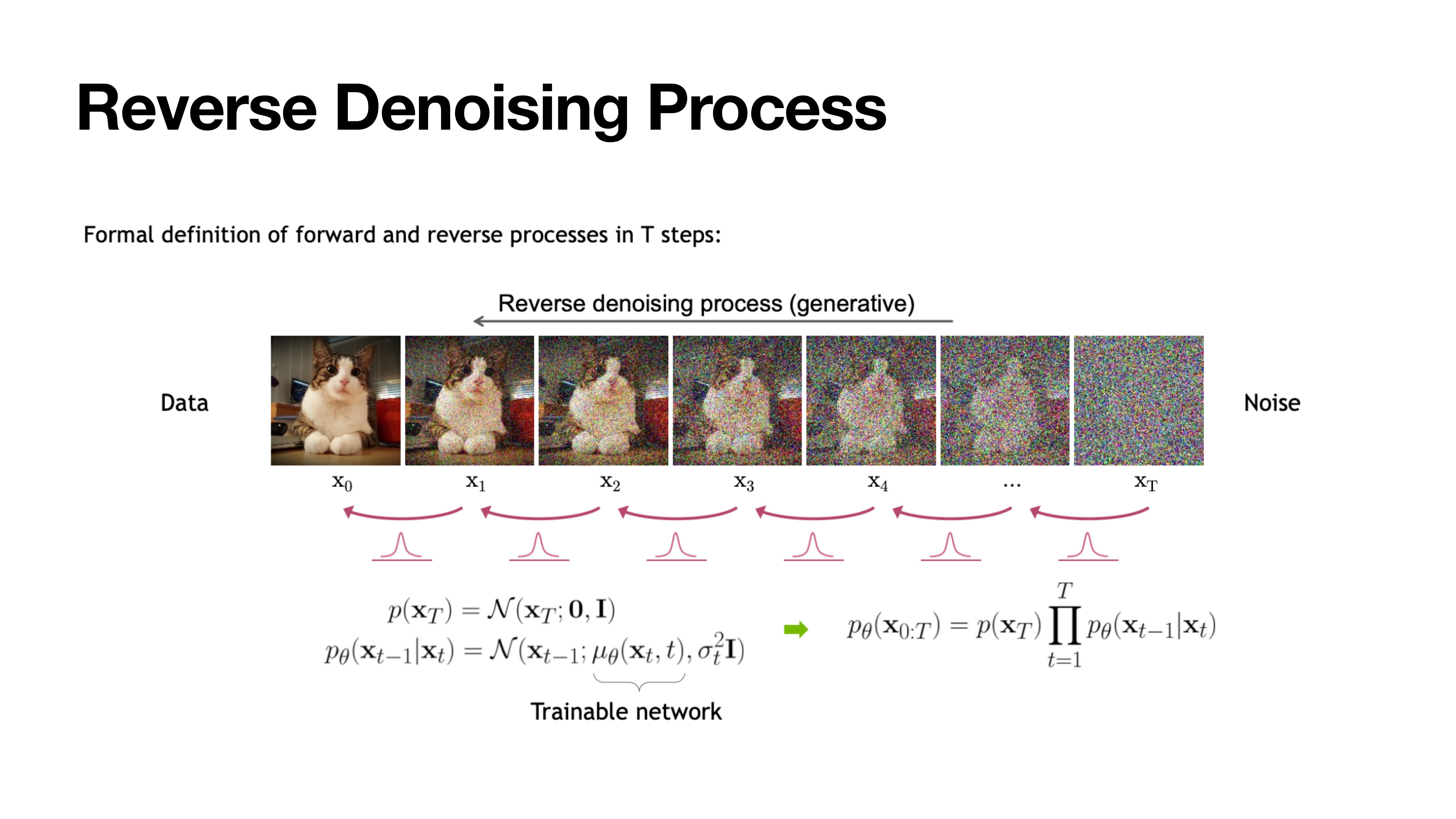
하지만 $q(\mathbf{x}_{t-1} \rvert \mathbf{x}_t)$는 알 수 없기에 이를 딥러닝으로 푼다.

Gaussian인 $p_{\theta}(\mathbf{x}_{t-1} \rvert \mathbf{x}_t)$의 평균과 분산을 추정한다.
(물론 분산은 Constant이기 때문에 추정하지 않는다. 자세한 내용은 뒤쪽에 설명)

Diffusion Kernel

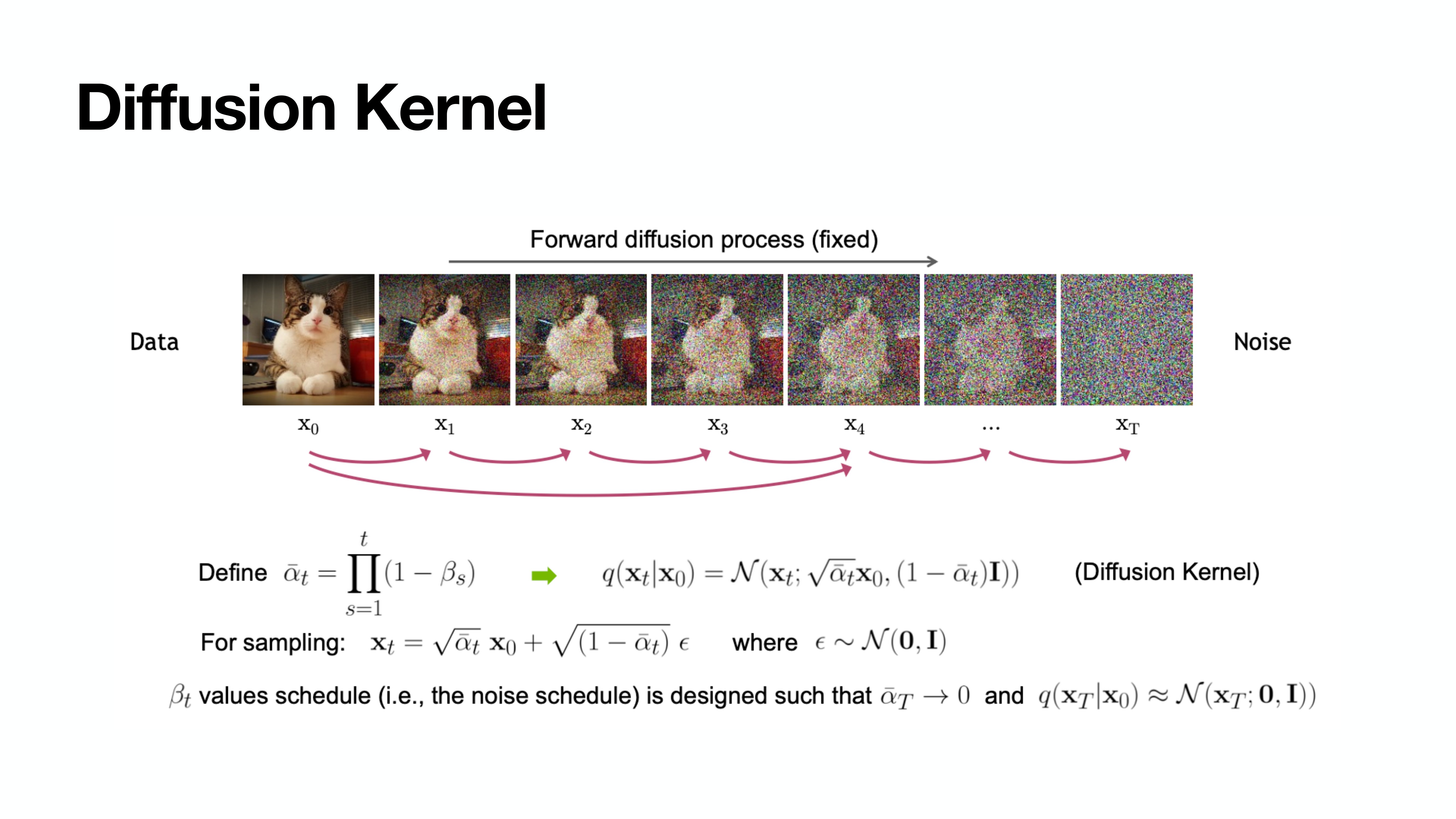
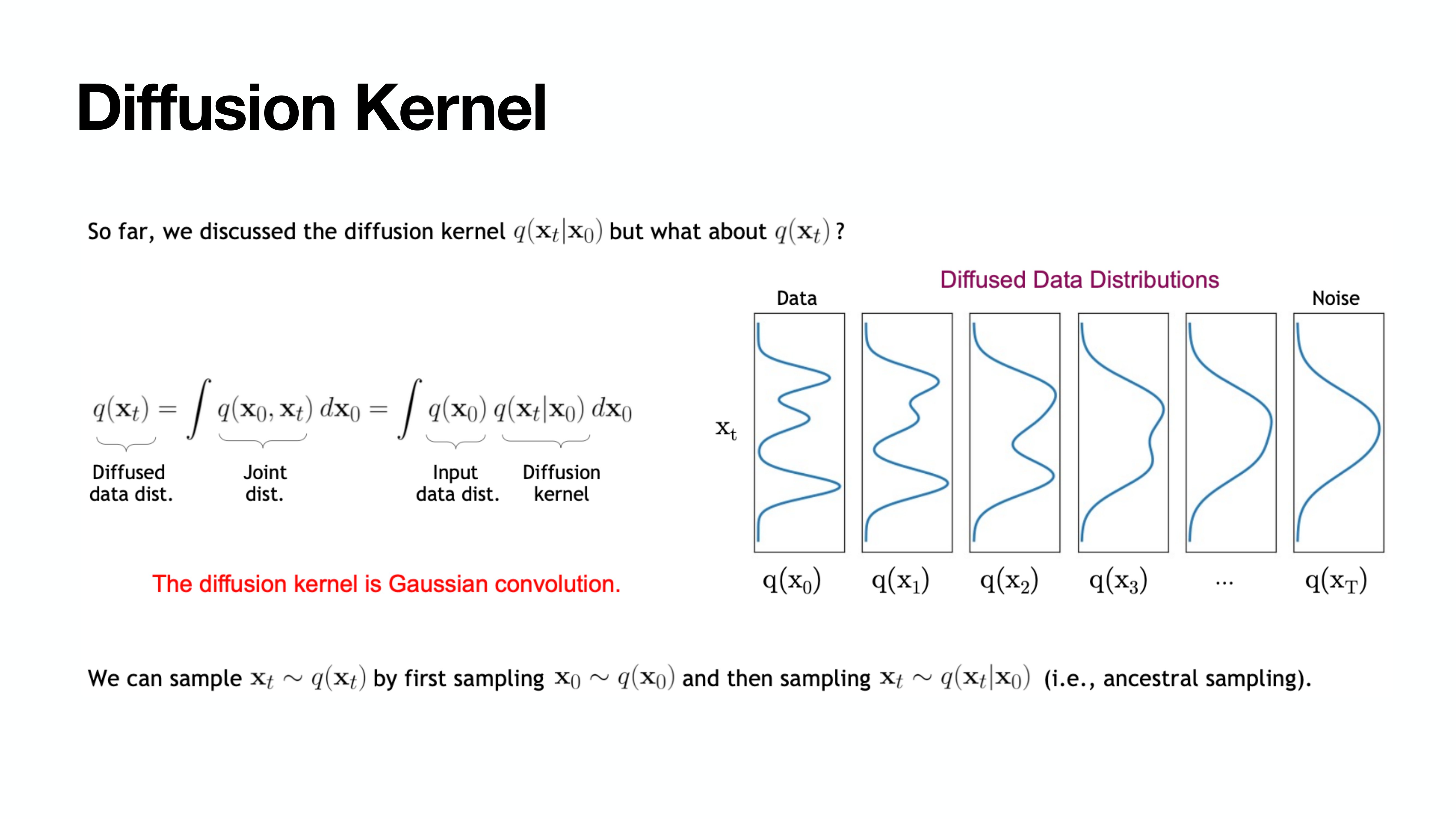
이렇게 굳이 loop를 거치지 않고도 $\mathbf{x}_0$가 주어졌을 때 한번에 $\mathbf{x}_t$를 구할 수 있다.

Generarive Learning by Denoising

이제부터 “어떻게 $q(\mathbf{x}_{t-1} \rvert \mathbf{x}_t)$를 추정할 수 있을까”에 대한 이야기이다.

뒤에 이어질 내용은 Varational Inference를 통해 ELBO를 만들고 이를 Loss로 활용하게 된다는 내용이다.

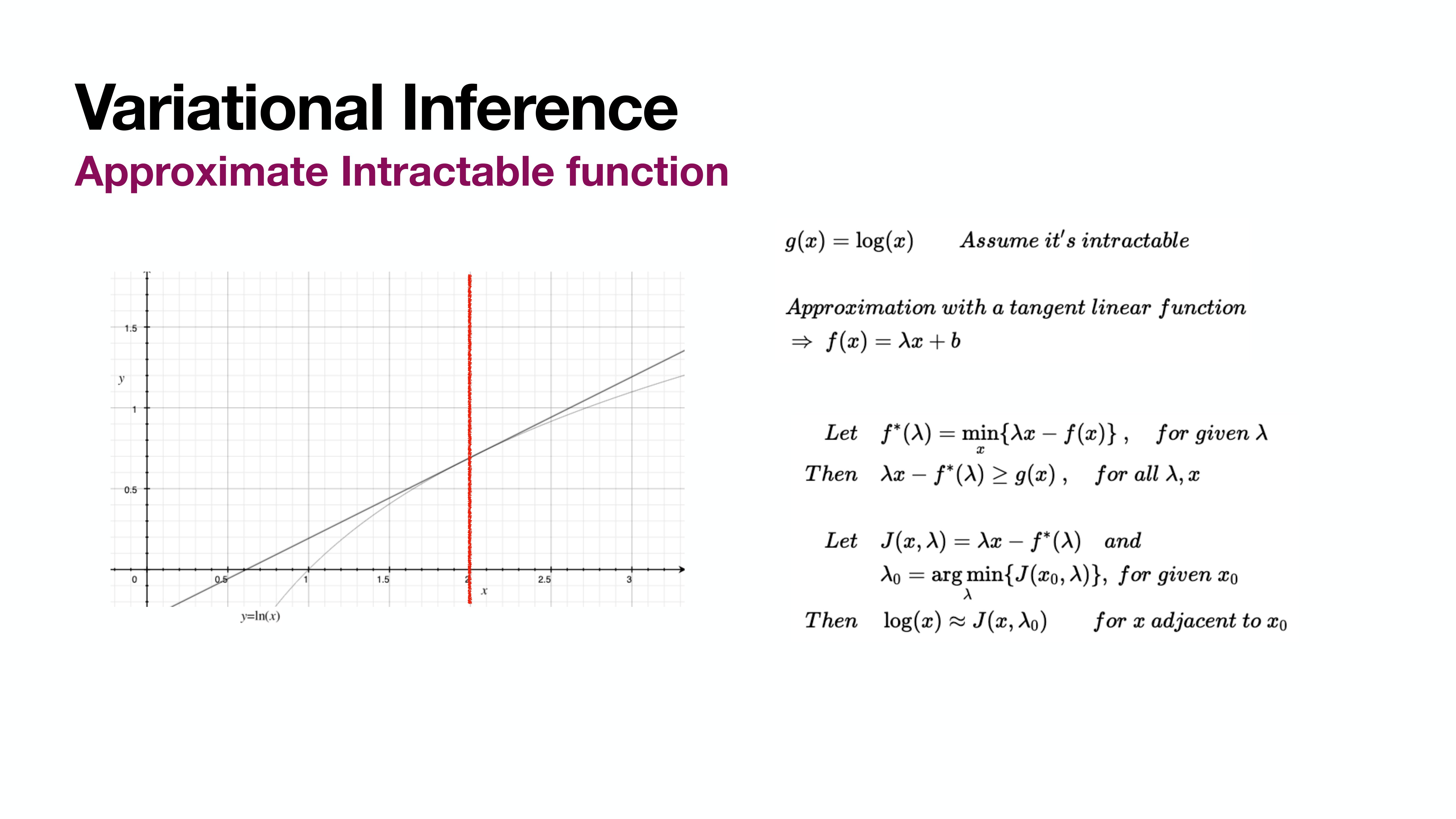
Varational Inference

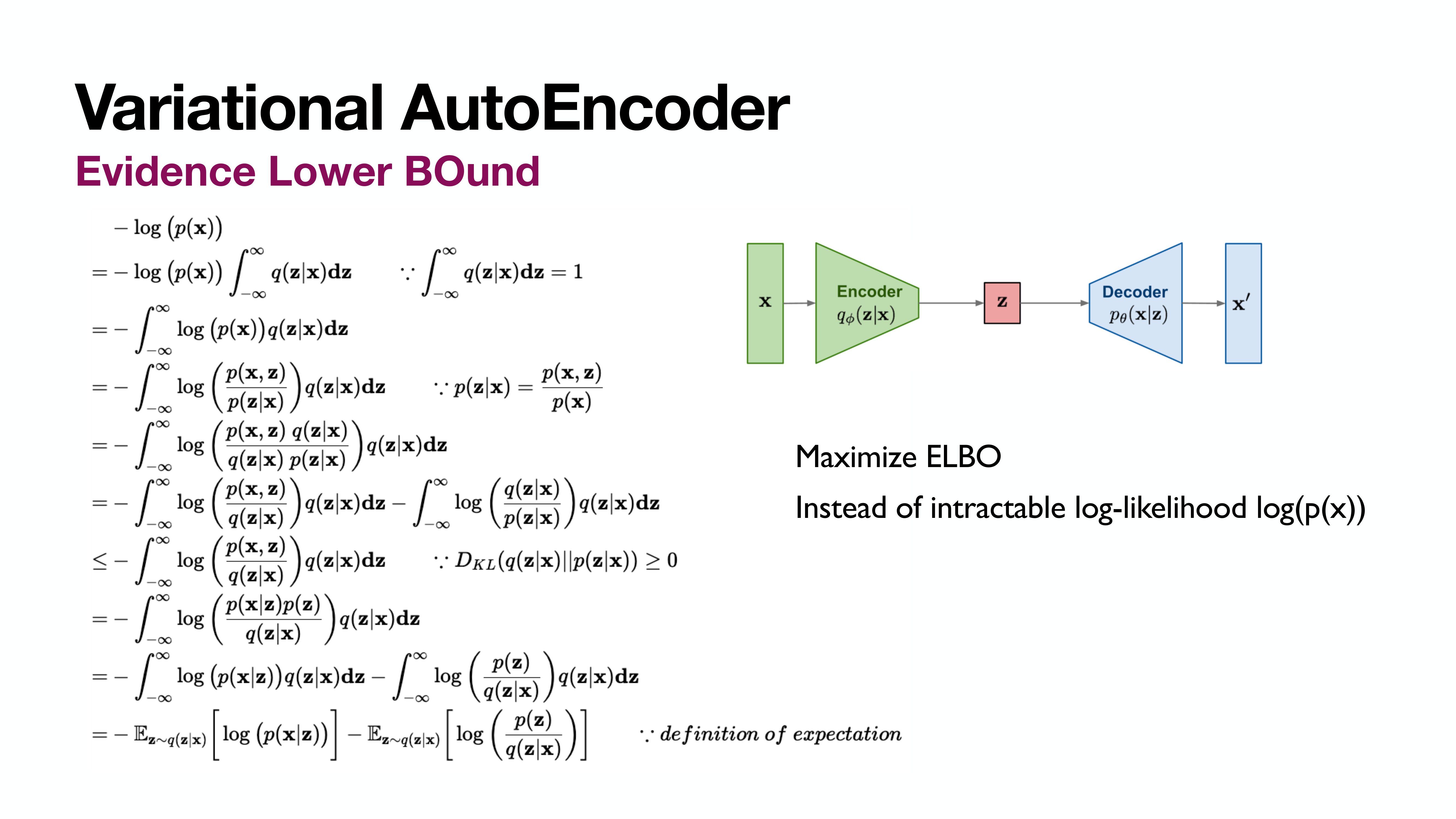
ELBO for VAE

ELBO for DDPM

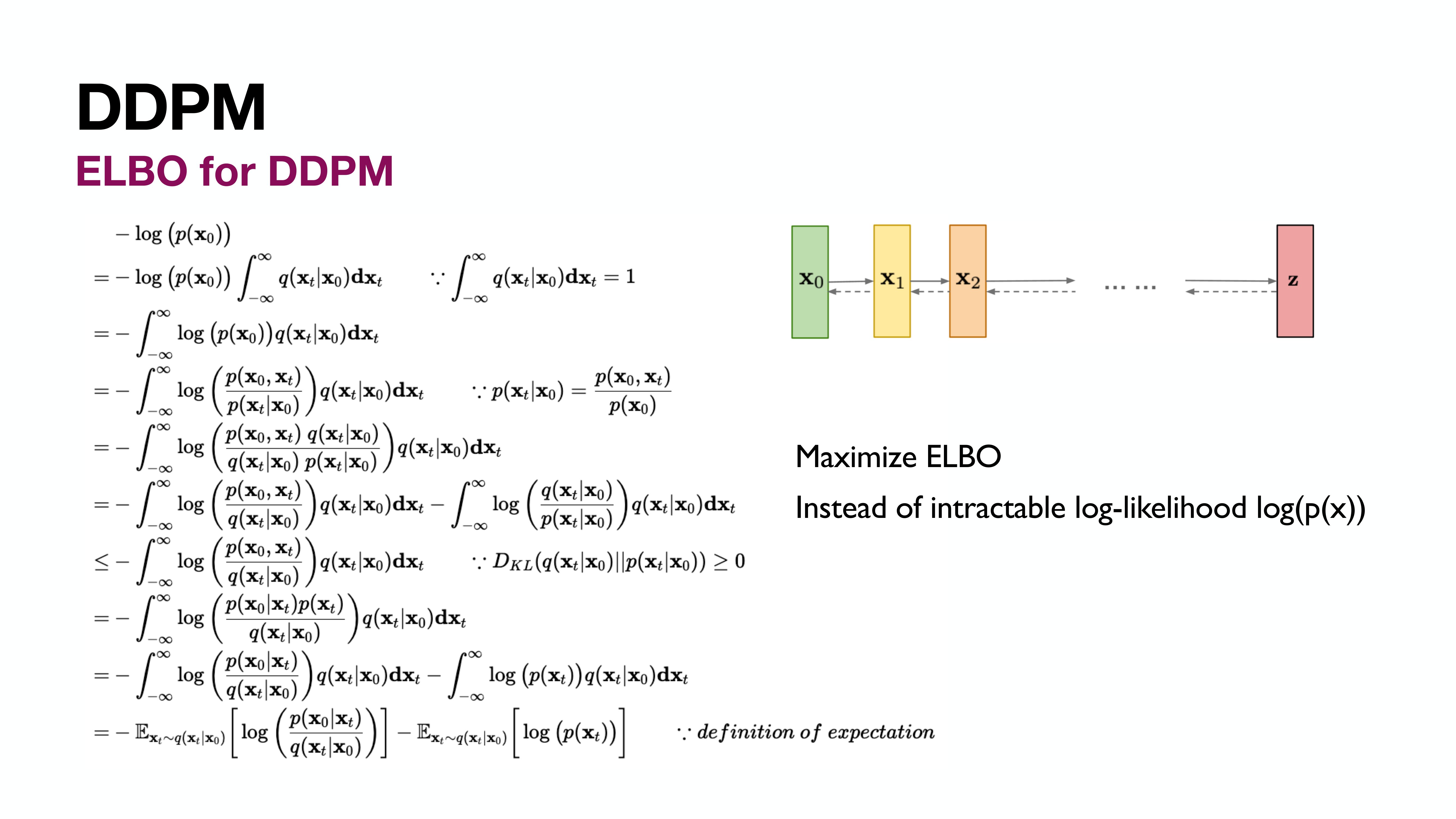
VAE의 ELBO와의 차이를 유심히 보면 좋다. 아래에서 두번째 line의 항 분리가 다르다. (VAE의 reconstruction loss를 떼내는 부분)

Loss

가장 마지막 line을 보면 $\sum$의 분모에 우리가 추정하고 싶은 $q(\mathbf{x}_{t-1} \rvert \mathbf{x}_{t})$가 아니라 $q(\mathbf{x}_{t} \rvert \mathbf{x}_{t-1})$이 있는 것을 볼 수 있다. (사실 있다해도 intractable하긴 하다.)

아래에서 이어질 수식 전개에는 Bayes’ rule을 이용하여 이를 $\mathbf{x}_t$에 대한 분포가 아닌 분자와 같이 $\mathbf{x}_{t-1}$에 대한 분포로 바꾸기 위한 과정이 들어있다고 생각하고 수식을 보면 좋다.

가장 아래 line의 분리된 세개의 항을 각각 $L_T,\ L_{T-1},\ L_0$라고 칭한다.

이떄 $L_T$의 KL Divergence를 계산하는 두 분포는 모두 $N(0, I)$로 같다. 따라서 $L_T$는 0이다.

$L_0$는 $\mathbf{x}_1$이 주어졌을 때 $\mathbf{x}_0$을 뽑아내는 것으로 VAE의 reconstruction error와 같다고 보면 된다. (본 포스트에서 이는 자세히 다루지 않는다.) 다만 차이가 있다면 VAE는 하나의 latent variable $\mathbf{z}$에서 바로 reconstruction을 수행하는 형태지만 Diffusion은 가장 $\mathbf{x}_0$에 가까운 $\mathbf{x}_1$에서 복원을 수행하는 것으로 모델 입장에서는 조금 더 쉽다고 할 수 있겠다.

중요하게 바라볼 것은 $L_{T-1}$이다.
우리는 결국 만드는 모델의 output이 $p_{\theta}(\mathbf{x}_{t-1} \rvert \mathbf{x}_t)$의 평균과 분산을 예측하도록 하면 된다. 그렇다면 label로 사용할 정답은 무엇인가? 바로 앞에 있는 $q(\mathbf{x}_{t-1} \rvert \mathbf{x}_t, \mathbf{x}_0)$의 평균과 분산이다.

$q(\mathbf{x}_{t-1} \rvert \mathbf{x}_t, \mathbf{x}_0)$의 평균과 분산은 위와 같이 계산된다. (수식유도는 Appendix에 적어두었다.)

이 때 $\tilde{\beta}_t$는 $\beta$를 설정함에 따라 정해진 Constant로 구할 수 있다. 즉 정답값을 언제나(inference시에도) 알 수 있으므로 추정할 필요가 없다.

하지만 $\tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0)$에는 inference시에는 알 수 없는 $\mathbf{x}_0$가 들어있다. 따라서 평균은 추정을 해야한다.

그런데 $\tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0)$는 $\mathbf{x}_0$를 $\mathbf{x}_t$를 이용해 나타냄으로써 한번 더 간단하게 정리가 가능하다. (자세한 수식은 마찬가지로 Appendix에)

이때 $\tilde{\mu}(\mathbf{x}_t, \mathbf{x}_0)$의 새로운 식에 모르는 값은 $\epsilon$외에 없다. 따라서 우리가 만들게 될 모델은 $\mathbf{x}_t$와 $t$를 input으로 받아 $\epsilon$을 추정하게 된다. $\mu$ 자체를 예측하는 방법도 있지만 논문의 ablation study에 따르면 $\epsilon$을 예측하는 것보다 성능이 떨어진다.

이때 $L_{T-1}$를 정리하면 나오는 앞의 상수 $\lambda_t$는 사용하지 않는다. $t$가 작아짐에 따라 $L_{T-1}$는 작아지게 되는데 이는 $\mathbf{x}_0$에 가까워질수록 Loss에 낮은 가중치가 붙는다고 할 수 있다. $\lambda_t$를 1로 고정하는 것이 sample quality에 더 좋다.

최종적으로 사용되는 $L_{T-1}$은 위의 $L_{sample}$과 같다. 다시봐도 놀랍고 아름답다. 수식을 통해 결국 우리가 딥러닝으로 예측해야하는 것은 $\epsilon$ 뿐임을 증명했다. 그리고 실제로 이렇게 하는 것만으로 Diffusion model은 학습이 잘 된다…
(튜토리얼 코드에서 $L_0$는 사용하지 않는다.)

Summary

Training과 Sampling(Inference)은 위 내용 그대로 하면 된다. 아래 예시 코드에 최대한 그대로 표현했다.

Training

Sample Generation

Tutorial Code

https://github.com/fidabspd/mywiki/blob/master/seminar/about_diffusion/diffusion_tutorial.ipynb

고려대학교 산업경영공학과 김정섭님 발표의 튜토리얼 코드를 상당히 참고해 만들었다.

References

• DDPM 논문
• Nvidia Google 발표
• 고려대학교 산업경영공학과 김정섭님 발표
• 연세대학교 권민기님 발표
• DDPM 설명 블로그
• Variational Inference 설명 블로그

슬라이드 자료는 Nvidia Google 발표를 많이 채용했고 슬라이드 흐름은 연세대학교 권민기님 발표를 가장 많이 참고했다.

감사합니다.

Appendix - Mathematical Expression

마무리

Langevin dynamics에 대해 잘 몰라서 논문에 해당 내용이 나올 때 좀 띄엄띄엄 읽게 되었다. 그래도 큰 흐름을 이해하는데는 문제가 없었지만 diffusion을 깊게 알고 싶다면 꼭 알아야 할 내용으로 보인다. Score와 관련이 있다고 하는데 해당 내용은 추가로 공부 예정.

Diffusion을 처음 접한다면 논문 읽기가 좀 까다롭지만 읽다보면 신기하고 놀랍다. 다들 직접 읽어보시길 추천.