Latent CNF를 이용한 mnist generator 제작기

얼마전 Voicebox 논문을 읽다가 NeuralODE를 접하게 되었다. 그렇게 NeuralODE 논문을 읽고 이를 주제로 사내 세미나를 진행하였다. NeuralODE는 NIPS 2018에서 Best paper로 선정된 논문이다. (논문 대한 리뷰 글은 아니기 때문에 생략. 리뷰 라기보단 사실 번역 참고.) 그리고 정말 어려운 논문이었다… 그래도 이제는! 완전히는 아니더라도 80% 정도는 이해했다고 말할 수 있을 것 같다.
그리고 NeuralODE에서 소개하는 CNF(Continuous Normalizing Flow)의 tutorial을 만들어 세미나 진행 당시 활용했다. (NeuralODE 공식 repo를 크게 참고했다.)

하지만 이 튜토리얼은 단순히 2차원 분포를 예측하는 것으로 너무 단순하다. 마침 세미나때도 이걸로 mnist generator 만드려면 어떻게 만드냐 는 질문이 들어왔다. 그래서 나는 단순하게 생각하면 28 x 28 (= 784) 차원으로 확대하면 된다. 라고 말했다. 그래서 세미나가 끝나고 아주 단순하게 mnist를 flatten해서 784차원 짜리 CNF 만들어보았는데.. 생각과는 좀 달랐다. hyper param을 수정하고 이것저것 네트워크를 만져봐도 forward에 1분 이상이 소비 됐다. (GTX 1080 Ti 기준.) 지금 생각해보면 그냥 뭔가 실수했던것 같기도 하고

그렇게 이미지를 그대로 CNF에 태우기 보다는, CNF의 차원을 줄여 Latent CNF만들기를 시작하게 되었다. 이에 대한 영감은 아래 두개의 생각에서 얻게 되었다.

1. VITS가 이와 비슷한 구조인데 이를 해봤던 경험을 살리고 싶었다.
2. latent diffusion의 등장으로 diffusion이 핫해졌던 것 처럼 나도 latent를 이용하고 싶었다.

Repository

코드는 여기서 확인하실 수 있습니다.

Trial 1. AE + CNF

Model

처음 구상한 아키텍쳐는 다음과 같다.

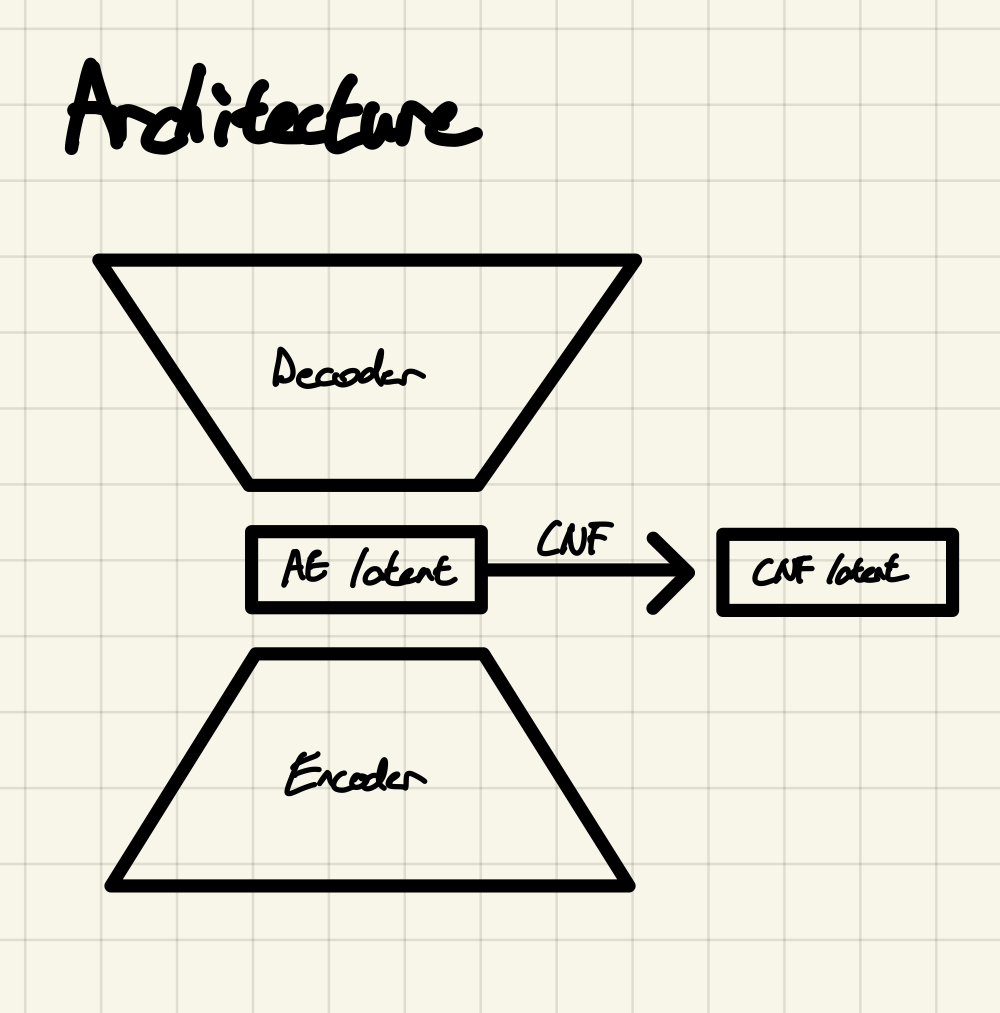
평범한 AutoEncoder의 latent에 CNF를 태우는 것이다. 나름 합리적이라고 생각했다.

인코더와 디코더는 지극히 평범한 MLP로 만들었고, CNF는 tutorial과 같이 만들었다. 모델 코드는 아래와 같다.

class ImageEncoder(nn.Module):
    def __init__(
        self,
        in_dim: int = 784,
        hidden_dim: int = 32,
        latent_dim: int = 2,
        n_hidden_layers: int = 2,
        epsilon: float = 1e-6,
        dropout_ratio: float = 0.1,
    ) -> None:
        super().__init__()
        self.hidden_dim = hidden_dim
        self.latent_dim = latent_dim
        self.epsilon = epsilon
        self.linear_in = nn.Linear(in_dim, hidden_dim)
        self.linear_hidden = nn.ModuleList([nn.Linear(hidden_dim, hidden_dim) for _ in range(n_hidden_layers)])
        self.linear_out = nn.Linear(hidden_dim, latent_dim)
        self.dropout = nn.Dropout(dropout_ratio)

    def forward(self, input: torch.Tensor) -> torch.Tensor:
        output = torch.flatten(input, start_dim=1)
        output = self.dropout(torch.relu(self.linear_in(output)))
        for layer in self.linear_hidden:
            output = self.dropout(torch.relu(layer(output)))
        output = self.linear_out(output)
        return output


class ImageDecoder(nn.Module):
    def __init__(
        self,
        latent_dim: int = 2,
        hidden_dim: int = 32,
        out_dim: int = 784,
        n_hidden_layers: int = 2,
        dropout_ratio: float = 0.1,
    ) -> None:
        super().__init__()
        self.out_dim = out_dim
        self.hidden_dim = hidden_dim
        self.linear_in = nn.Linear(latent_dim, hidden_dim)
        self.linear_hidden = nn.ModuleList([nn.Linear(hidden_dim, hidden_dim) for _ in range(n_hidden_layers)])
        self.linear_out = nn.Linear(hidden_dim, out_dim)
        self.dropout = nn.Dropout(dropout_ratio)

    def forward(self, input: torch.Tensor) -> torch.Tensor:
        output = self.dropout(torch.relu(self.linear_in(input)))
        for layer in self.linear_hidden:
            output = self.dropout(torch.relu(layer(output)))
        output = torch.sigmoid(self.linear_out(output))
        output = output.view(-1, 1, int(self.out_dim**0.5), int(self.out_dim**0.5))
        return output


class HyperNetwork(nn.Module):
    """https://arxiv.org/abs/1609.09106"""

    def __init__(self, in_out_dim, hidden_dim, width):
        super().__init__()

        blocksize = width * in_out_dim

        self.linear_hidden_0 = nn.Linear(1, hidden_dim)
        self.linear_hidden_1 = nn.Linear(hidden_dim, hidden_dim)
        self.linear_out = nn.Linear(hidden_dim, 3 * blocksize + width)

        self.in_out_dim = in_out_dim
        self.hidden_dim = hidden_dim
        self.width = width
        self.blocksize = blocksize

    def forward(self, t):
        # predict params
        params = t.reshape(1, 1)
        params = torch.tanh(self.linear_hidden_0(params))
        params = torch.tanh(self.linear_hidden_1(params))
        params = self.linear_out(params)

        # restructure
        W = params[:, : self.blocksize].reshape(-1, self.width, self.in_out_dim, 1).transpose(0, 1).contiguous()

        U = (
            params[:, self.blocksize : 2 * self.blocksize]
            .reshape(-1, self.width, 1, self.in_out_dim)
            .transpose(0, 1)
            .contiguous()
        )

        G = (
            params[:, 2 * self.blocksize : 3 * self.blocksize]
            .reshape(-1, self.width, 1, self.in_out_dim)
            .transpose(0, 1)
            .contiguous()
        )
        U = U * torch.sigmoid(G)

        B = params[:, 3 * self.blocksize :].reshape(-1, self.width, 1, 1).transpose(0, 1).contiguous()
        return [W, B, U]


class ODEFunc(nn.Module):
    def __init__(self, in_out_dim, hidden_dim, width):
        super().__init__()
        self.in_out_dim = in_out_dim
        self.hidden_dim = hidden_dim
        self.width = width
        self.hyper_net = HyperNetwork(in_out_dim, hidden_dim, width)

    def trace_df_dz(self, f, z):
        """Calculates the trace (equals to det) of the Jacobian df/dz."""
        sum_diag = 0.0
        for i in range(z.shape[1]):
            sum_diag += torch.autograd.grad(f[:, i].sum(), z, create_graph=True)[0].contiguous()[:, i].contiguous()

        return sum_diag.contiguous()  # [batch_size]

    def forward(self, t, states):
        z, logp_z = states
        batchsize = z.shape[0]

        with torch.set_grad_enabled(True):
            z.requires_grad_(True)

            W, B, U = self.hyper_net(t)

            Z = z.unsqueeze(0).unsqueeze(-2).repeat(self.width, 1, 1, 1)

            h = torch.tanh(torch.matmul(Z, W) + B)
            dz_dt = torch.matmul(h, U).mean(0)  # mean by width dim
            dz_dt = dz_dt.squeeze(dim=1)

            dlogp_z_dt = -self.trace_df_dz(dz_dt, z).view(batchsize, 1)

        return (dz_dt, dlogp_z_dt)


class AECNF(nn.Module):
    def __init__(
        self,
        batch_size: int = 64,
        in_out_dim: int = 784,
        hidden_dim: int = 32,
        latent_dim: int = 2,
        n_hidden_layers: int = 2,
        ode_t0: int = 0,
        ode_t1: int = 10,
        cov_value: float = 0.1,
        ode_hidden_dim: int = 64,
        ode_width: int = 64,
        dropout_ratio: float = 0.1,
        device: str = "cuda:0",
    ) -> None:
        super().__init__()
        self.batch_size = batch_size
        self.device = device
        self.t0 = ode_t0
        self.t1 = ode_t1
        self.latent_dim = latent_dim

        # pdf of z0
        mean = torch.zeros(latent_dim).type(torch.float32)
        cov = torch.zeros(latent_dim, latent_dim).type(torch.float32)
        cov.fill_diagonal_(cov_value)
        self.p_z0 = torch.distributions.MultivariateNormal(
            loc=mean.to(self.device), covariance_matrix=cov.to(self.device)
        )

        self.image_encoder = ImageEncoder(
            in_dim=in_out_dim,
            hidden_dim=hidden_dim,
            latent_dim=latent_dim,
            n_hidden_layers=n_hidden_layers,
            dropout_ratio=dropout_ratio,
        )
        self.image_decoder = ImageDecoder(
            latent_dim=latent_dim,
            hidden_dim=hidden_dim,
            out_dim=in_out_dim,
            n_hidden_layers=n_hidden_layers,
            dropout_ratio=dropout_ratio,
        )
        self.ode_func = ODEFunc(
            in_out_dim=latent_dim,
            hidden_dim=ode_hidden_dim,
            width=ode_width,
        )

    def forward(self, input: torch.Tensor) -> Tuple[torch.Tensor]:

        z_t1 = self.image_encoder(input)
        reconstructed = self.image_decoder(z_t1)

        logp_diff_t1 = torch.zeros(self.batch_size, 1).type(torch.float32).to(self.device)
        z_t, logp_diff_t = odeint(
            self.ode_func,
            (z_t1, logp_diff_t1),
            torch.tensor([self.t1, self.t0]).type(torch.float32).to(self.device),  # focus on [T1, T0] (not [T0, T1])
            atol=1e-5,
            rtol=1e-5,
            method="dopri5",
        )
        z_t0, logp_diff_t0 = z_t[-1], logp_diff_t[-1]

        logp_x = self.p_z0.log_prob(z_t0).to(self.device) - logp_diff_t0.view(-1)

        return reconstructed, logp_x

    def generate(self, n_time_steps: int = 2) -> Tuple[torch.Tensor]:
        with torch.no_grad():
            z_t0 = self.p_z0.sample([1]).to(self.device)
            logp_diff_t0 = torch.zeros(1, 1).type(torch.float32).to(self.device)

            time_space = np.linspace(self.t0, self.t1, n_time_steps)  # [T0, T1] for generation
            z_t_samples, _ = odeint(
                self.ode_func,
                (z_t0, logp_diff_t0),
                torch.tensor(time_space).to(self.device),
                atol=1e-5,
                rtol=1e-5,
                method="dopri5",
            )
            z_t_samples = z_t_samples.view(n_time_steps, -1)
            gen_image = self.image_decoder(z_t_samples)

        return gen_image, time_space

Loss

Loss는 AE 훈련을 위한 reconstruction error와 CNF 훈련을 위한 negative likelihood를 사용했다.

class FinalGeneratorLoss(nn.Module):
    def __init__(
        self,
        recon_loss_weight: float = 1.0,
        cnf_loss_weight: float = 1.0,
        return_only_final_loss: bool = True,
    ) -> None:
        super().__init__()
        self.recon_loss_weight = recon_loss_weight
        self.cnf_loss_weight = cnf_loss_weight
        self.return_only_final_loss = return_only_final_loss
    
    def calculate_recon_loss(
        self, image_true: torch.Tensor, image_pred: torch.Tensor
    ) -> torch.Tensor:
        recon_loss = image_true * torch.log(image_pred + 1e-7) + (1 - image_true) * torch.log(1 - image_pred + 1e-7)
        recon_loss = torch.flatten(recon_loss, start_dim=1).sum(dim=1).mean()
        return recon_loss

    def calculate_cnf_loss(self, logp_x: torch.Tensor) -> Tuple[torch.Tensor]:
        log_prob = logp_x.mean()
        loss = -log_prob
        return loss, log_prob

    def forward(
        self,
        image_true: torch.Tensor,
        image_pred: torch.Tensor,
        logp_x: torch.Tensor,
    ) -> Union[torch.Tensor, Tuple[torch.Tensor]]:
        recon_loss = self.calculate_recon_loss(image_true, image_pred)
        cnf_loss, cnf_log_prob = self.calculate_cnf_loss(logp_x)
        final_generator_loss = (
            - self.recon_loss_weight * recon_loss
            + self.cnf_loss_weight * cnf_loss
        )
        if self.return_only_final_loss:
            return final_generator_loss
        else:
            return (
                final_generator_loss,
                recon_loss,
                cnf_log_prob,
            )

학습시에 recon_loss_weight와 cnf_loss_weight의 설정이 중요했다. 둘에 차이를 두지 않고 1로 설정할 경우 학습이 제대로 되지 않았다. 이에 시행착오를 겪고 recon_loss_weight=3.0, cnf_loss_weight=0.1의 값을 설정하였다.

Training

latent diffusion에 대해 잘 아는 것은 아니지만 (논문은 읽어보지 않았고 몇몇 블로그의 리뷰 포스트를 읽어봤다. 잘 봤던 포스트) VAE를 먼저 훈련해놓고 Freeze한 뒤에 해당 VAE의 Encoder에 input을 넣고 latent를 뽑아 해당 latent를 label로 diffusion을 훈련하는 2-stage training을 한다고 알고있다. 개인적으로 2-stage보다 1-stage training을 좋아하기 때문에 1-stage로 훈련했다.

Generation Result

시각화를 위해 아래 함수를 사용했다.

def visualize_inference_result(
    z_t_samples: torch.Tensor,
    time_space: np.array,
    save_dirpath: str,
    global_step: int,
) -> None:
    if not os.path.exists(save_dirpath):
        os.makedirs(save_dirpath)

    fig, ax = plt.subplots(1, 11, figsize=(22, 1.8))
    for i in range(11):
        t = time_space[i]
        z_sample = z_t_samples[i].view(28, 28)
        ax[i].imshow(z_sample.detach().cpu())
        ax[i].set_axis_off()
        ax[i].set_title("$$p(\mathbf{z}_{" + str(t) + "})$$")
    save_filename = f"infer_{global_step}.png"
    plt.savefig(os.path.join(save_dirpath, save_filename), dpi=300, bbox_inches="tight")
    plt.close()

cnf튜토리얼과 마찬가지로 11단계로 cnf를 시각화하였다. \(t_0\)는 0, \(t_1\)은 10으로 0 ~ 10까지의 정수일 때의 \(z\)를 ImageDecoder에 태워 latent를 image 형태로 변환하여 시각화 한다. 그 결과는 아래와 같다.

정확히 예상했던 결과를 얻었다.

\(z_{t_0} \sim \mathcal{N}(0, I),\ z \in \mathbb{R}^2\)로 설정하였으므로 (사실 \(I\)가 아니라 diag가 0.1인 diag matrix로 설정했지만 편의상 그냥 \(I\)라고 하자. 거기서 거기다.) CNF를 거치지 않은 \(z_0\)를 ImageDecoder에 태울 시, 숫자가 아닌 이상한 모양을 만들어낼 수도, 예쁜 숫자를 만들어 낼 수도 있다. 그리고 cnf를 거치면서 AE의 latent 분포에 매칭되므로 \(z_{10}\)을 ImageDecoder에 태우면 숫자가 생성된다.

Latent Visualization

이제 latent를 시각화 해보자. 이를 위해 latent dim을 2로 설정하였다.

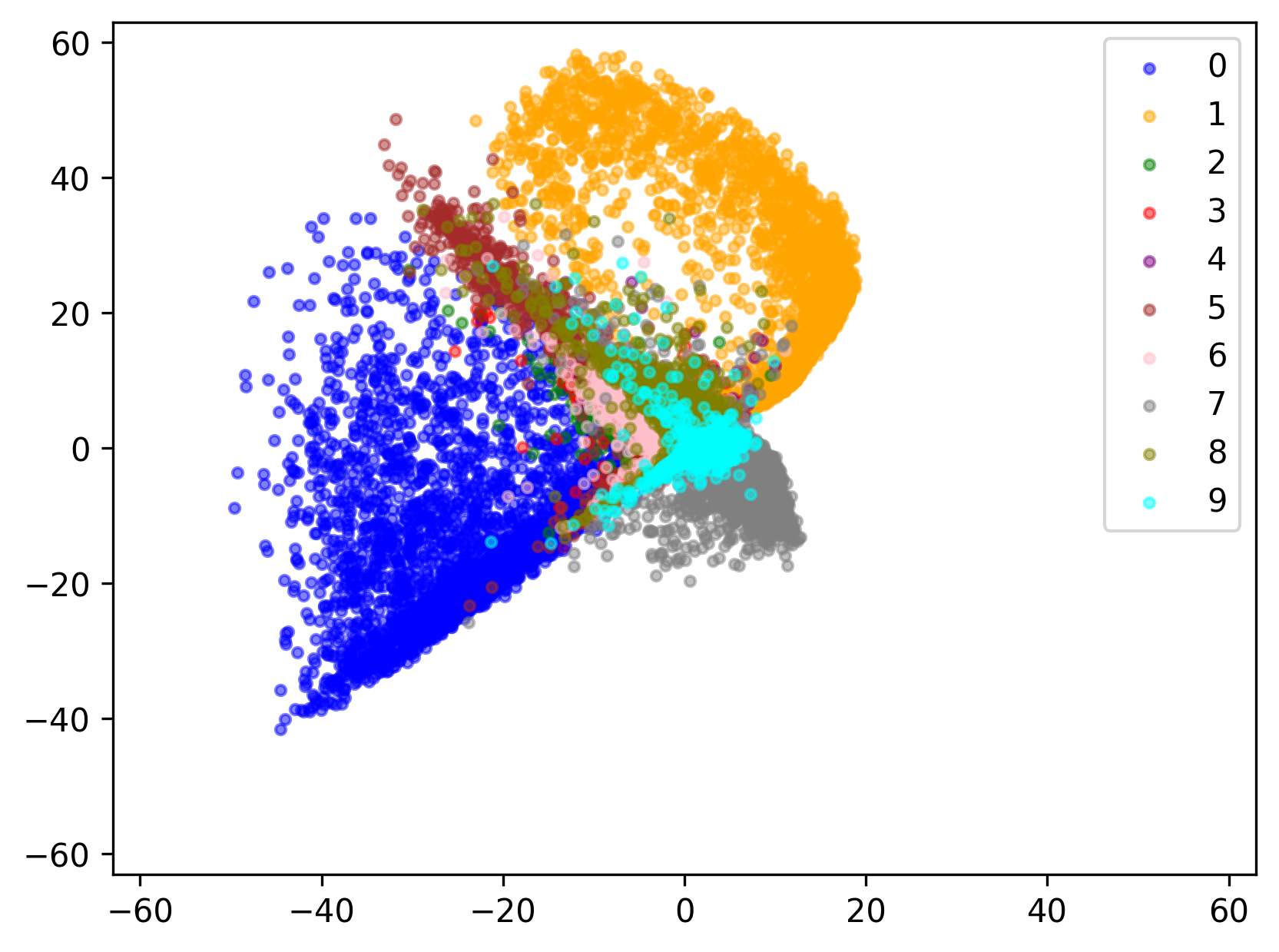
완벽하지는 않지만 나쁘지 않다. 숫자들마다 latent가 적절히 구성되었다.

\(z_{t_0} \sim \mathcal{N}(0, I)\)가 CNF를 탄 결과인 \(z_{t_1}\)도 시각화 해보자. label을 condition으로 활용하지는 않았기 때문에 숫자별 구분은 무의미하다. 따라서 하나의 색으로만 살펴보도록 하자. 전체적인 분포의 모양이 위와 비슷해야 제대로 된 결과라고 할 수 있을 것이다.

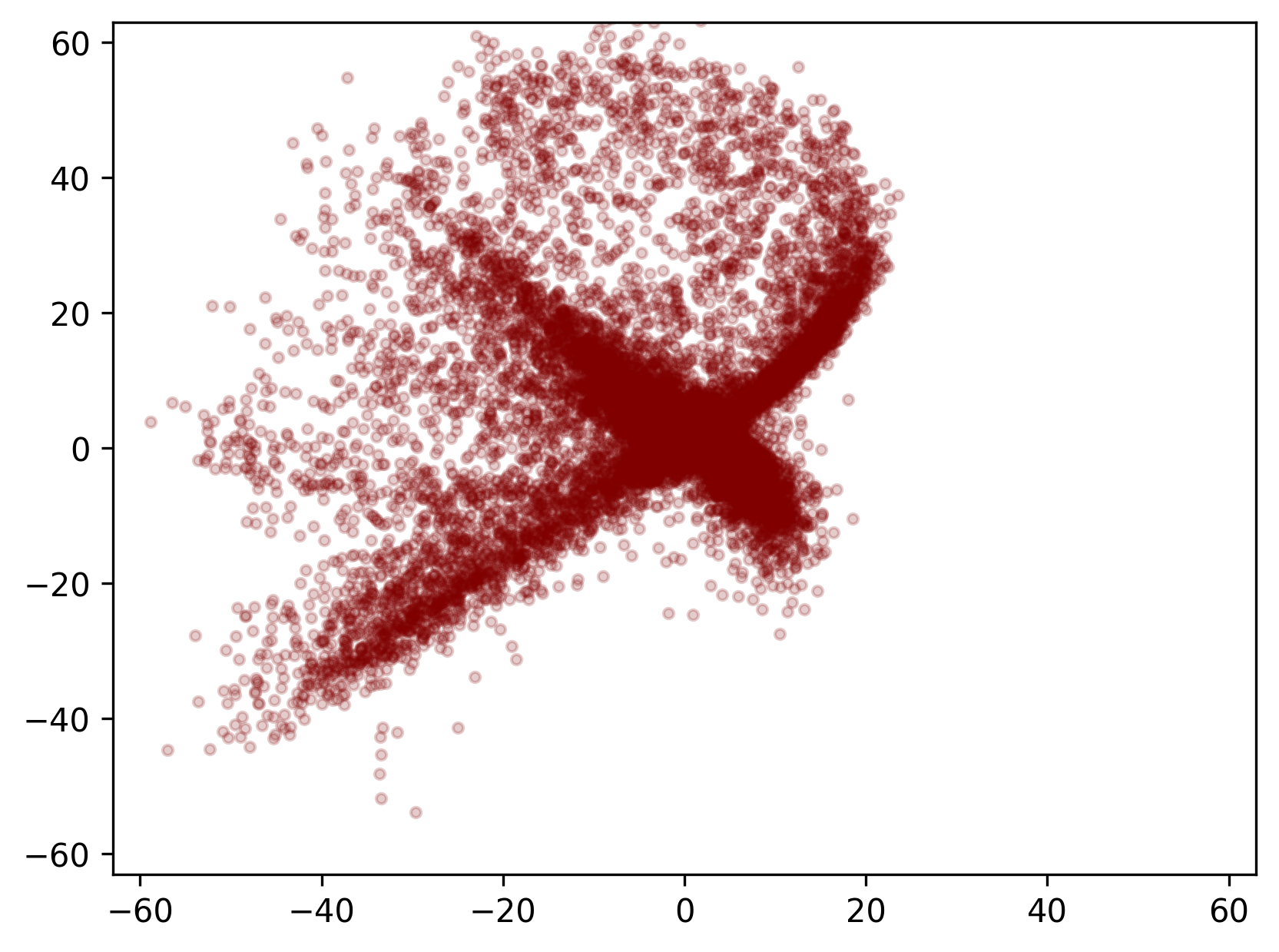
아주 잘됐다. 1-stage 훈련에 성공했다. 만족스럽다 후훗.

Trial 2. VAE + CNF (ver1)

여기까지 완성하고나서 든 생각은 지금은 괜찮지만 AE만을 사용하니 latent가 너무 제멋대로의 모양으로 넓게 분포하게 된 것이 불안했다. 지금은 괜찮았지만, 학습이 진행됨에 따라 AE의 latent가 퍼지는 속도를 CNF가 따라가지 못한다면 CNF는 제대로 학습이 되지 않을 것이다. 그러면 1-stage로 학습을 구성한 것에 문제가 생길 수도 있다고 판단했다. 따라서 VAE를 사용해보고 싶어졌다. VAE를 적용하기 위해서 KL divergence를 어떻게 구성할지가 가장 고민이었다.

이게 고민이었던 이유는 두가지이다.

1. 그냥 단순하게 VAE의 ELBO를 그대로 사용하고, CNF loss를 그대로 사용하면 CNF를 굳이 사용할 이유가 있나 싶었다. VAE latent 그냥 random sampling해서 ImageDecoder 태우면 generation이 가능할테니까.
2. 일반적인 VAE와 ELBO를 다르게 사용한다면, prior distribution을 뭐로 설정할 것이냐에 대한 고민이 있었다. 이는 Trial 3에서 자세하게 설명한다.

일단은 일반적인 ELBO를 사용해보도록 하자.

latent diffusion은 reconstruction을 더욱 잘 수행하기 위해 KL divergence에 \(10^{-6}\)등의 아주 작은 가중치를 사용했다. 이에 착안하여 recon_loss_weight=3.0, kl_divergence_weight=1.0, cnf_loss_weight=0.1을 사용하였다. kl_divergence_weight=1.0의 이유는 그냥 너무 작은 수는 하고싶지 않았다. 아마 \(10^{-6}\)정도의 작은 수를 사용하면 AE보다는 조금 덜 퍼지는 분포를 가지게 되지 않을까.

VAE 형태를 띄도록 모델에서는 Encoder만 변경하였고 loss에 KL divergence를 추가했다. 간단한 변경이고 이 외에는 변경이 없으므로 코드는 생략.

Generation Result

성공했다.

Latent Visualization

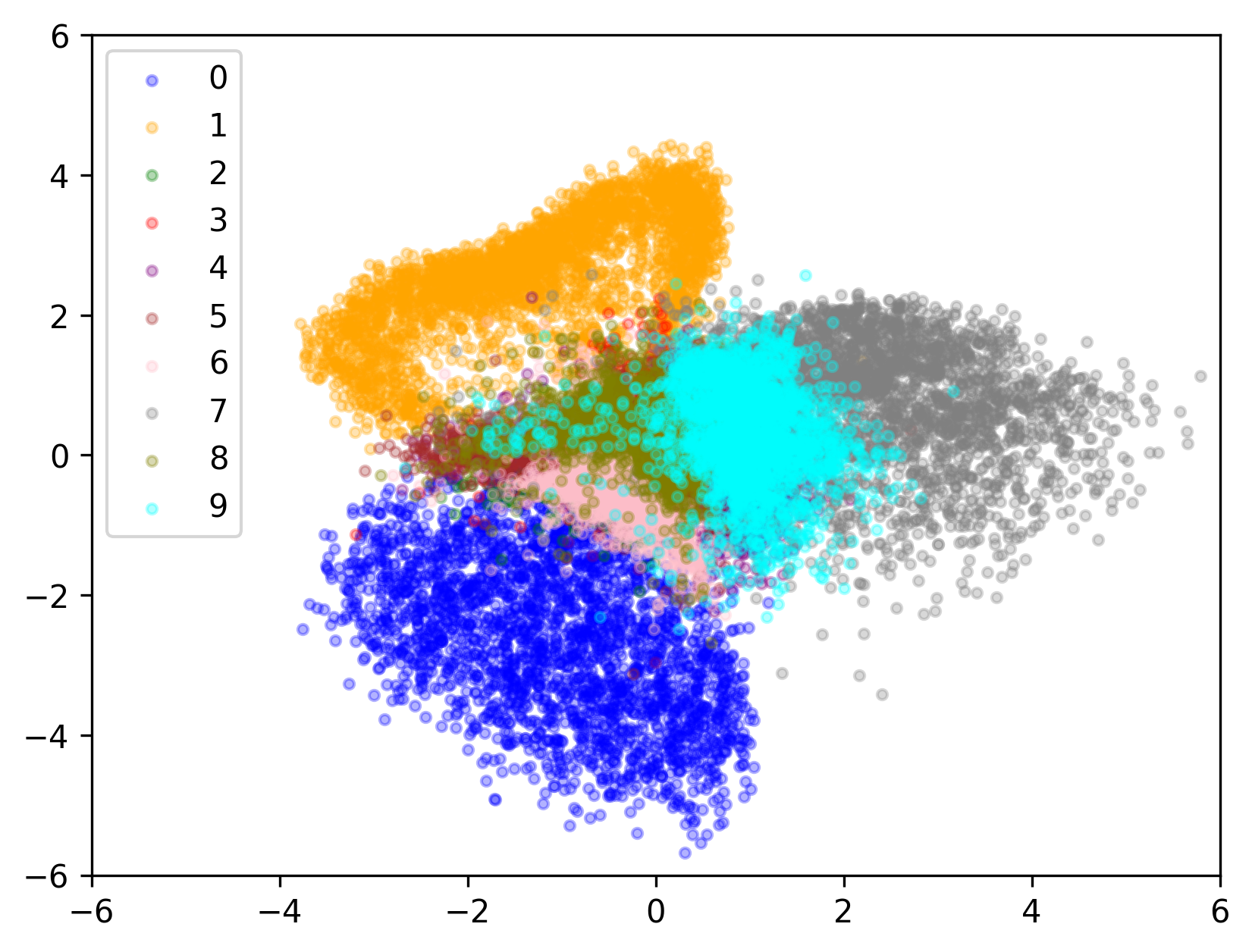
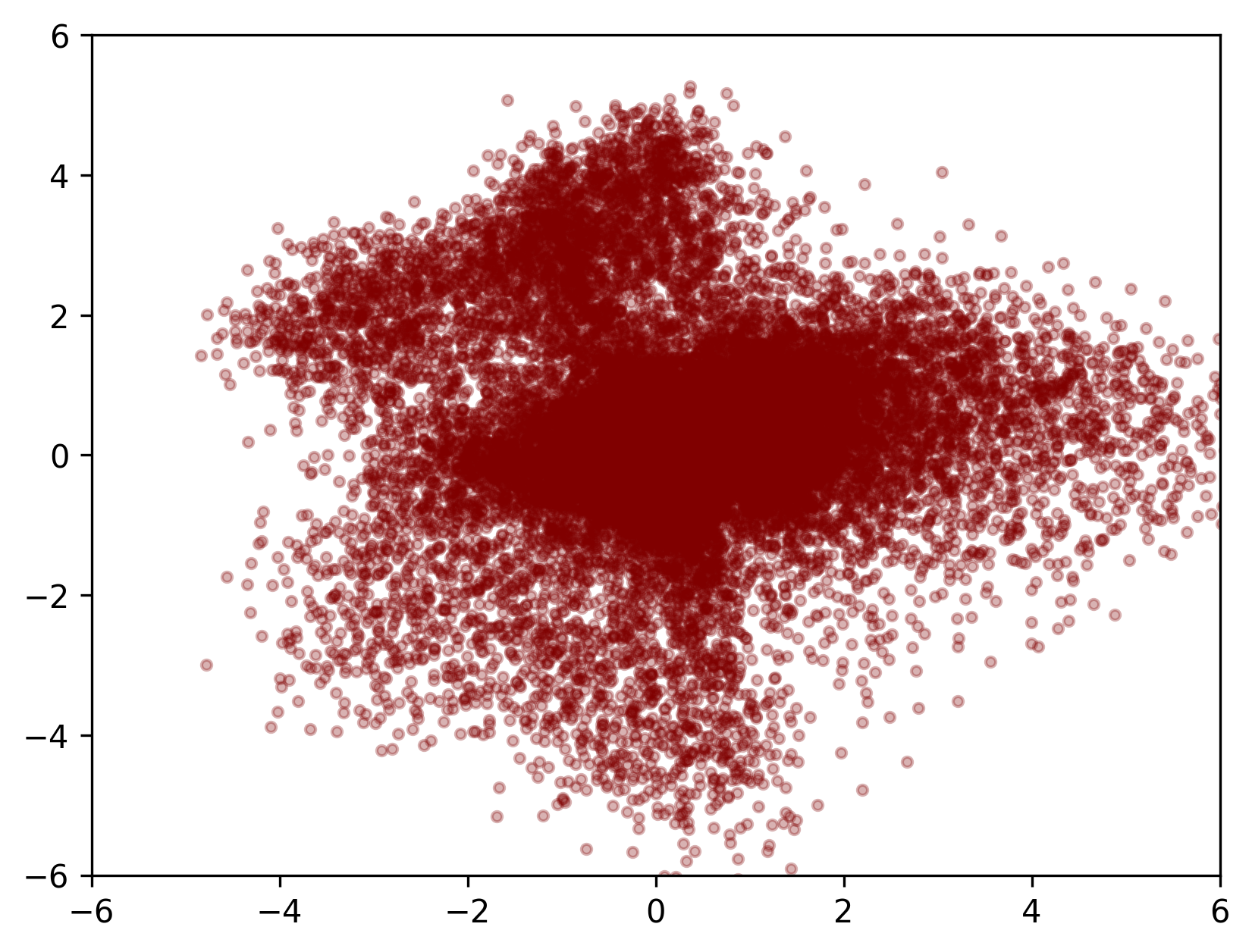
완전한 정규분포의 형태로 나타나지는 않았지만 의도했던대로 만들어졌다. 넓게 퍼진 분포를 줄였고 CNF도 성공적으로 학습되었다.

Trial 3. VAE + CNF (ver2)

Trial 3는 Trial 2에서 말한 일반적인 VAE와 ELBO를 다르게 사용한다면, prior distribution을 뭐로 설정할 것이냐 의 고민의 과정이다.

우선 일반적인 VAE ELBO와 KL divergence는 다음과 같다.

\[\begin{align*} & \int \log (p(\mathbf{x}\vert\mathbf{z})) q(\mathbf{z}\vert\mathbf{x}) d\mathbf{z} - \int \log \Big( \dfrac{q(\mathbf{z}\vert\mathbf{x})}{p(\mathbf{z})} \Big) q(\mathbf{z}\vert\mathbf{x}) d\mathbf{z} \\ =\ & \mathbb{E}_{\mathbf{z} \sim q(\mathbf{z}\vert\mathbf{x})} \Big[ \log(p(\mathbf{x}\vert\mathbf{z})) \Big] - \mathbb{E}_{\mathbf{z} \sim q(\mathbf{z}\vert\mathbf{x})} \Big[ \log \Big( \dfrac{q(\mathbf{z}\vert\mathbf{x})}{p(\mathbf{z})} \Big) \Big] \quad \because\ definition\ of\ expectation \\ \end{align*}\] \[\begin{align*} KL =\ & \mathbb{E}_{\mathbf{z} \sim q(\mathbf{z}\vert\mathbf{x})} \Big[ \log \Big( \dfrac{q(\mathbf{z}\vert\mathbf{x})}{p(\mathbf{z})} \Big) \Big] \\ =\ & \mathbb{E}_{\mathbf{z} \sim q(\mathbf{z}\vert\mathbf{x})} \Big[ \log q(\mathbf{z}\vert\mathbf{x}) \Big] - \mathbb{E}_{\mathbf{z} \sim q(\mathbf{z}\vert\mathbf{x})} \Big[ \log p(\mathbf{z}) \Big] \end{align*}\]

그리고 보통 \(q(\mathbf{z} \vert \mathbf{x})\) 를 Gaussian, \(\mathbf{z} \sim \mathcal{N}(0, I)\) 를 가정하기 때문에 KL divergence는 두 정규분포의 KL divergence 계산에 따라 아래와 같다. (두 정규분포간의 KLD 자세한 유도 참고)

\[\begin{align*} KL(q \Vert p) =\ & \log \Big( \dfrac{\sigma_p}{\sigma_q} \Big) + \dfrac{\sigma_q^2 + (\mu_q - \mu_p)^2}{2\sigma_p^2} - \dfrac{1}{2} \\ =\ & \dfrac{1}{2} \Big( -2\log \sigma_q + \sigma_q^2 + \mu_q^2 - 1 \Big) \end{align*}\]

이를 현재 상황에 대입해본다면, 당연히 \(\mathbf{x}\)는 원래의 이미지, \(\mathbf{z}\)는 latent이다. 본 모델은 VAE와 CNF를 둘 다 사용하기 때문에 VAE의 latent와 CNF의 latent를 구분해야한다. CNF입장에서는 VAE의 latent가 생성해내야하는 target이기 때문에 앞으로 VAE의 latent를 \(\mathbf{z}_{t_1}\), CNF의 latent를 \(\mathbf{z}_{t_0}\)라고 하자. 그리고 당연히 위 ELBO식에서 \(\mathbf{z}\)는 \(\mathbf{z}_{t_1}\)를 의미한다. 하지만 이게 prior가 \(p(\mathbf{z}_{t_1})\)라는 의미가 될 수 있을까?

Generation(Inference)시에 모델의 시작은 VAE가 아닌 CNF부터 이루어진다. 즉 원칙대로라면 prior는 \(p(\mathbf{z}_{t_1})\) 가 아니라 \(p(\mathbf{z}_{t_1} \vert \mathbf{z}_{t_0})\)이 맞다. (\(\mathbf{z}_{t_0} \sim \mathcal{N}(0, I)\)) 따라서 KL을 아래와 같이 바꿀 수 있다.

\[\begin{align*} KL =\ & \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log \Big( \dfrac{q(\mathbf{z}_{t_1}\vert\mathbf{x})}{p(\mathbf{z}_{t_1}\vert\mathbf{z}_{t_0})} \Big) \Big] \\ =\ & \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log q(\mathbf{z}_{t_1}\vert\mathbf{x}) \Big] - \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log p(\mathbf{z}_{t_1}\vert\mathbf{z}_{t_0}) \Big] \end{align*}\]

그런데 여기서 문제가 있는데, \(p(\mathbf{z}_{t_1}\vert\mathbf{z}_{t_0})\) 의 \(\mu_p, \sigma_p\) 를 무슨수로 구할 것이냐는 점이다. 그리고 이게 애초에 Gaussian이 맞긴 한가? 하는 생각도 든다.

따라서 두 Gaussian 간의 KLD 계산 공식인 \(\log \Big( \frac{\sigma_p}{\sigma_q} \Big) + \frac{\sigma_q^2 + (\mu_q - \mu_p)^2}{2\sigma_p^2} - \frac{1}{2}\) 는 사용하지 않기로 했다.

Loss

그 대신 \(\mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log q(\mathbf{z}_{t_1}\vert\mathbf{x}) \Big] - \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log p(\mathbf{z}_{t_1}\vert\mathbf{z}_{t_0}) \Big]\) 이것을 비슷하게나마 사용해보자. 먼저 첫째항은 아래와 같이 정리가 가능하다.

\[\begin{align*} & \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log q(\mathbf{z}_{t_1}\vert\mathbf{x}) \Big] \\ = & \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ \log \Big( \dfrac{1}{\sigma_q \sqrt{2\pi}} e^{-\dfrac{1}{2} \big( \dfrac{\mathbf{z}_{t_1} - \mu_q}{\sigma_q} \big)^2} \Big) \Big] \\ = & \mathbb{E}_{\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})} \Big[ -\log\sigma_q -\dfrac{1}{2}\log(2\pi) - \dfrac{1}{2} \big( \dfrac{\mathbf{z}_{t_1} - \mu_q}{\sigma_q} \big)^2 \Big] \\ = & -\log\sigma_q -\dfrac{1}{2}\log(2\pi) - \dfrac{\mathbb{E}(\mathbf{z}_{t_1}^2) - 2\mathbb{E}(\mathbf{z}_{t_1})\mu_q + \mu_q^2}{2\sigma_q^2} \\ = & -\log\sigma_q -\dfrac{1}{2}\log(2\pi) - \dfrac{\sigma_q^2 + \mu_q^2 - 2\mu_q^2 + \mu_q^2}{2\sigma_q^2} \quad \because \sigma_q^2 = \mathbb{E}(\mathbf{z}_{t_1}^2) - \mu_q^2\\ = & -\log\sigma_q -\dfrac{1}{2}\log(2\pi) - \dfrac{1}{2} \\ \end{align*}\]

둘째항은 \(\log p(\mathbf{z}_{t_1}\vert\mathbf{z}_{t_0})\) 를 직접 계산하는 것이 가능하다. CNF의 loss자체가 이와 같기 때문이다. 다만 이를 그냥 평균을 내게 되면 \(\mathbf{z}_{t_1} \sim q(\mathbf{z}_{t_1}\vert\mathbf{x})\) 에 대한 평균은 아닐 것이다. 그래도 일단 해보자.

새로운 KL divergence에 대한 코드는 아래와 같이 사용했다.

def calculate_kl_divergence(
    self, posterior_std: torch.Tensor, prior_log_probs: torch.Tensor
) -> torch.Tensor:
    posterior_log_probs = (
        -torch.log(posterior_std)
        - 0.5 * torch.log(2 * torch.FloatTensor([torch.pi]).to(posterior_std.device))
        - 0.5
    )
    posterior_log_probs = posterior_log_probs.sum(dim=1)  # assume non diagonal elements of cov matrix are zero
    kl_divergence = posterior_log_probs - prior_log_probs
    kl_divergence = kl_divergence.mean()
    return kl_divergence

그리고 원래 사용하던 cnf_loss는 제외했다. 이유는 KLD에 이미 완전히 똑같은 항이 포함되었기 때문이다.

또한 ImageEncoder에서 사용된 relu들을 tanh로 바꿨다. 이유는 prior를 바꾸면서 posterior의 분포가 Gaussian으로 수렴하도록 유도할 무언가가 없어져버린 상황에서 그나마 최대한 symmetric한 형태를 유지하기 위해서였다.

Generation Result

개인적으로 논리가 좀 어설픈 구석이 있다고 생각했지만 잘 나왔다.

Latent Visualization

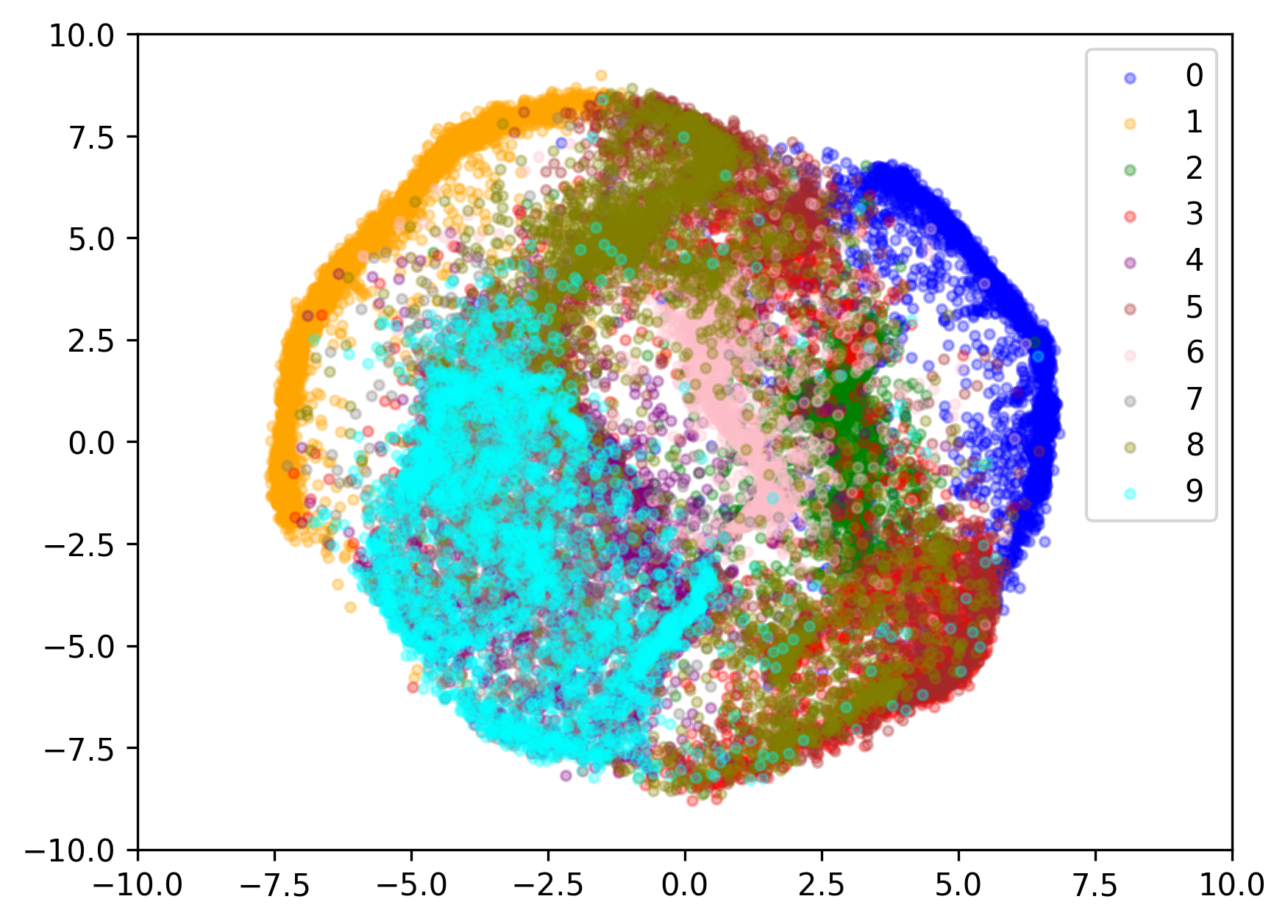
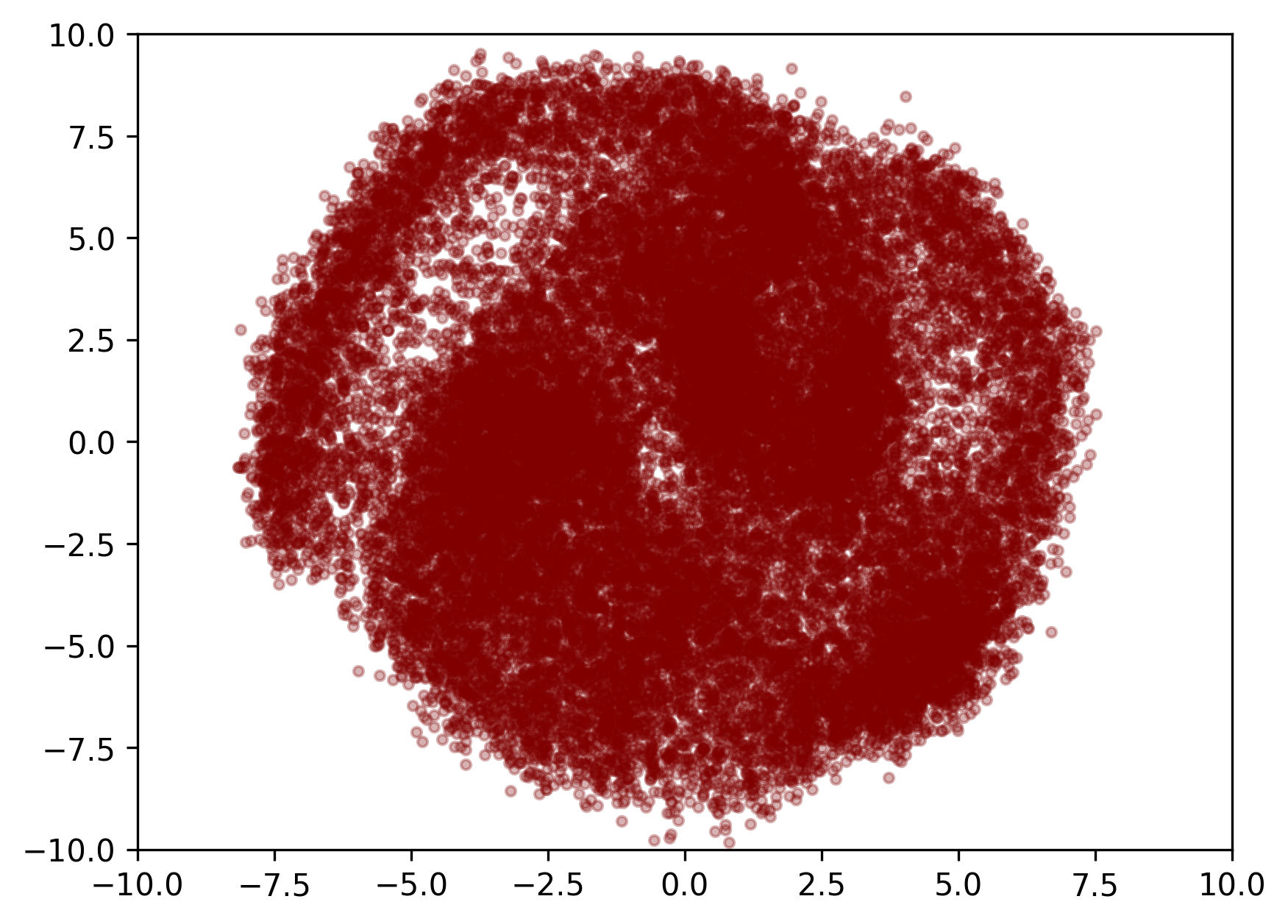
구멍이 너무 송송 뚫려있긴하지만 어쨌든 cnf는 학습이 잘 된 것으로 보인다.

Final Version

조금 아쉬워서 Trial 3에서 몇가지를 추가하기로 했다.

Discriminator

Discriminator를 추가했다. 사실 Flow 기반 모델은 Adversarial Loss를 사용하기에는 적절하지는 않다고 생각한다. 그 이유는 아래와 같다.

현재 모델 기준 Training시의 Fake 이미지는 실제로 Generated된 이미지가 아니다. 정확히는 Encoder로 생성된 Latent를 Decoder로 Reconstruct한 이미지이다. Training 과정에서 실제로 Inference를 수행하여 Generated된 이미지를 Discriminator의 Fake이미지로 활용하는게 아니면 CNF는 Discriminator로 인한 이득을 볼 수 없다. 그래도 Decoder를 더 정교하게 만드는 효과정도는 있을 것이라고 생각된다. 앞서 말한대로 하면 CNF에도 사용은 할 수 있을 것 같긴 하다. 다만 효과적일지는 잘 모르겠다. layer 구성은 아래와 같다.

class PartDiscriminator(nn.Module):
    def __init__(
        self,
        in_channels: int = 1,
        hidden_channels: int = 32,
        out_channels: int = 1,
        kernel_size: int = 3,
        stride: int = 1,
    ) -> None:
        super().__init__()
        conv0 = nn.Conv2d(in_channels, hidden_channels, kernel_size, stride, padding="same")
        conv1 = nn.Conv2d(hidden_channels, hidden_channels, kernel_size, stride, padding="same")
        conv2 = nn.Conv2d(hidden_channels, hidden_channels, kernel_size, stride, padding="same")
        self.conv_layers = nn.ModuleList([conv0, conv1, conv2])
        self.post_layer = nn.Conv2d(hidden_channels, out_channels, kernel_size, stride)

    def forward(self, input) -> Tuple[torch.Tensor, List[torch.Tensor]]:
        feature_maps = []
        for layer in self.conv_layers:
            input = layer(input)
            feature_maps.append(input)
        output = torch.sigmoid(self.post_layer(input))
        return output, feature_maps


class FullDiscriminator(nn.Module):
    def __init__(
        self,
        in_channels: int = 1,
        hidden_channels: int = 32,
        out_channels: int = 1,
        stride: int = 1,
    ) -> None:
        super().__init__()
        discriminators = []
        for kernel_size in (3, 5):
            discriminator = PartDiscriminator(
                in_channels=in_channels,
                hidden_channels=hidden_channels,
                out_channels=out_channels,
                kernel_size=kernel_size,
                stride=stride,
            )
            discriminators.append(discriminator)
        self.discriminators = nn.ModuleList(discriminators)

    def forward(self, input: torch.Tensor) -> Tuple[List[torch.Tensor]]:
        outputs = []
        feature_maps = []
        for discriminator in self.discriminators:
            output, feature_map = discriminator(input)
            outputs.append(output)
            feature_maps.extend(feature_map)
        return outputs, feature_maps

정확히 훈련에 어떻게 사용했는지는 repo에서 보는 것이 더 편합니다.

Latent Dimension 확장

지금까지는 Latent 시각화를 위해서 dimension을 2로 고정했었다. 하지만 이제는 학습 잘 되는거 알았으니까 조금더 구분감 있는 manifold를 만들기 위해 dimension을 8로 늘렸다.

Encoder Condition

manifold를 더 잘 만들기 위해 latent를 8로 늘렸지만 조금 허전하니 ImageEncoder에 label condition을 추가했다. condition layer의 구성과 사용은 아래와 같다.

class TanhSigmoidMultiplyCondition(nn.Module):
    def __init__(
        self,
        hidden_dim: int = 2,
    ) -> None:
        super().__init__()
        self.hidden_dim = hidden_dim

    def forward(self, input: torch.Tensor, condition: torch.Tensor) -> torch.Tensor:
        in_act = input + condition
        t_act = torch.tanh(in_act[:, : self.hidden_dim])
        s_act = torch.sigmoid(in_act[:, self.hidden_dim :])
        output = t_act * s_act
        return output


class ImageEncoder(nn.Module):
    def __init__(
        self,
        in_dim: int = 784,
        condition_dim: int = 4,
        hidden_dim: int = 32,
        latent_dim: int = 2,
        n_hidden_layers: int = 2,
        epsilon: float = 1e-6,
        dropout_ratio: float = 0.1,
    ) -> None:
        super().__init__()
        self.hidden_dim = hidden_dim
        self.latent_dim = latent_dim
        self.epsilon = epsilon
        self.linear_in = nn.Linear(in_dim, hidden_dim * 2)
        self.linear_condition = nn.Linear(condition_dim, hidden_dim * 2 * n_hidden_layers)
        self.linear_hidden = nn.ModuleList([nn.Linear(hidden_dim, hidden_dim * 2) for _ in range(n_hidden_layers)])
        self.linear_out = nn.Linear(hidden_dim * 2, latent_dim * 2)
        self.condition_mix_layer = TanhSigmoidMultiplyCondition(hidden_dim)
        self.dropout = nn.Dropout(dropout_ratio)

    def forward(self, input: torch.Tensor, condition: torch.Tensor) -> Tuple[torch.Tensor]:
        output = torch.flatten(input, start_dim=1)
        output = self.linear_in(output)
        condition = self.linear_condition(condition)
        for i, layer in enumerate(self.linear_hidden):
            condition_seg = condition[:, i * self.hidden_dim * 2 : (i + 1) * self.hidden_dim * 2]
            output = self.condition_mix_layer(output, condition_seg)
            output = self.dropout(torch.tanh(layer(output)))
        output = self.linear_out(output)
        mean, std = torch.split(output, self.latent_dim, dim=1)
        std = torch.exp(std) + self.epsilon
        output = mean + torch.randn_like(mean) * std
        return output, mean, std

Generation Result

괜찮게 잘 나왔다.

결론 + 추가적인 고찰

AE의 latent가 퍼지는 속도를 CNF가 따라가지 못한다면 CNF는 제대로 학습이 되지 않을 것이다. 라고 Trial 1이 끝나는 시점에 언급하였지만, 사실 이건 VAE를 쓴 Trial 2 역시도 마찬가지다. 다만 Trial 3부터는 애초에 prior를 기존과는 다르게 설정했기 때문에 이를 방지할 수 있을 것으로 생각된다. 하지만 솔직히 latent diffusion의 방식처럼 2-stage로 학습하면 이런걱정 하지 않아도 된다. 개인적으로 Trial 3의 논리가 완벽하다고 생각되지 않기 때문에 조금 아쉽다.

VITS가 이를 해결한 방법을 따라하고 싶었지만 NF가 아니라 CNF에서 이를 따라히기는 어려웠다.

그래도 나름의 논리로 성공적인 결과를 얻었으니 만족한다.

추가적으로

더 발전을 추구해본다면 해보고 싶은건 다음과 같다.

• CNF에 Label Condition 활용: CNF에 Condition을 사용하여 원하는 Label에 해당하는 latent에 찾아갈 수 있도록 하고싶다.
• 다른 이미지 사용: 일단은 fashion mnist로 해보면 어떨까 싶다. 잘 되려면 CNF에 Condition 사용이 선행되는 것이 좋을 것 같다.

Repository

코드는 여기서 확인하실 수 있습니다.